研究现状:
GIS位置服务的核心不外乎“在哪里”和“怎么走”两个核心部分,而我们生存的世界是三维的,因此人类有意识以来,对世界的感知就是多维的(二维和三维)。计算机科学的核心在于逻辑的“零和一”,随着计算机科学的发展,“零和一”这种思维造就多数学者面对需采用计算机科学技术解决的问题时首先想到的是如何在逻辑上完善它,进而通过算法实现的思维模式。这种思路的优势在于其是线型思维容易理解和逻辑严谨,实现难度不大,缺陷在于面对复杂的自然科学问题,采用传统的逻辑判断模式,而不结合自然界三维分布的特性进行思维上的拓展,则对于复杂自然科学问题的解决分析终究会走入死巷。
GIS空间科学的研究对象就是三维世界,因此空间科学研究人员天生就有多维思维的能力。众所周知,维度升级代表无限可能,维度降级意味着问题简单化。采用空间科学的视角看我们的世界,升维有助于我们解决问题探索世界,降维有助于我们简单化问题实现可行性操作,这也是我们科技工作者每天都在从事的工作。
以GIS测绘地理信息系统科学中的变形观测的为例,当我们运用即知因素去分析变形特征,发现偏差依然比较大,则可能存在如下可能:假定的影响因子不是等权或影响力不是线性的,或者是存在不知晓的其他影响因子,这就是当面对问题既有模型不能完美解决问题时,将思维拓展到多维(非线性影响或更多因子影响)时,问题的解决才成为可能。 在数百年前当数学家还为高次方运算如何化简困惑时,对数理论的出现使得问题迎刃而解。当面对三角函数等非线性函数的求解时,泰勒展开的出现使得人类可以用简单的线性函数求解非线性函数,降维使得问题解决简单化可操作。微分使得人类能够洞悉事物发展的趋势,积分使得人类具有用局部分析洞悉全局的可能,因此升维降维的空间科学思维一直在指引人类更好地理解我们的世界,是隐藏在人类科学研究中的隐性推手。
地理信息科学中位置服务是当前的热点问题,而位置服务中的“怎么走”属于最短路径分析的范畴。如果采用传统的数学、计算机图形学、生物学等模式分析,将会使得两个问题很难得到统一:“最优解但效率低”或“效率高但不确定最优”,依然没有完美的理论解决“最优”与“最快”的矛盾。这些理论多基于传统逻辑分析的范畴,其搜索的运算量至少与样本数存在二次方以上的相关性,因此在既有的理论框架下进行优化和拓展很难有实质性的突破,问题的解决需要研究人员拓展思维,尝试用其他方式理解和分析问题。
当解决了路径选择优化问题后,向前分析,连通性也就是目标点有路可通就成为问题解决的前提。因此可以将路径优化的理论稍作拓展,将道路可通、路径优化作为整体考虑,使得问题的解决由单一的优化拓展到联通分析、路径优化、应用扩展,再将路径优化拓展到多点之间、目标点自动选择、障碍物环境下的路径优化等领域,最终实现基于核心理论技术的立体创新应用。
解决思路

可能解的求解可以进行如下分析,如果目标点之间存在依次相邻的街区,则街区边界(路径)就可以作为可能解,基于此就将问题的线求解拓展到面领域,实现问题简化求解,如图 2 临近街区合并,初始解求得即图 2 加黑部分。
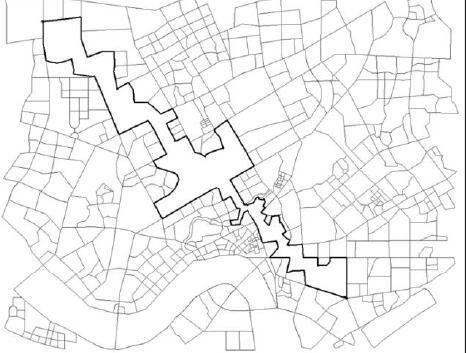
完成初始解的搜寻,下一步需要将初始解优化,由多边形的几何特性可知,多边形是闭合的连线,因此多边形上任意两点都有两条且仅有两条路径存在,类似于空间科学中的降维问题简化。基于此以目标点为起始,对可能的多边形进行组合和优化,得到最终的最短路径。完成搜索后,结果是否是最优解,可简单分析如下:当该路径上存在两点,其连接线大于既有的路径部分,则与上文优化过程冲突,持续优化直到结果最优。此外,根据图形学基本原理,对最终结果进行如下分析和优化,以最终结果长度为基准,以起终点为。
焦点构建椭圆,该范围外解存在可能性为零,将搜索范围固化在一定范围内,将全局搜索简化到局部搜索,确保了最优路径搜索实现过程的科学、准确、高效,解决了路径搜索中“快与准”的矛盾。同样,根据是否存在依次相连的街区,也可分析出是否目标点相连,实现搜索过程的完整科学高效。
完成两目标点点的路径分析,则将思维拓展到多目标点,结合测绘学原理,必经结点就如约束网求解,而从多个点中选出最佳目标点就是自由网求解,将如上两个问题进行拓展,同样采用空间科学思维,可以实现自由解问题的完美解决和必经结点的局部最优,将运筹学、逻辑学及计算机图形学中的经典难题运用空间科学的升维降维思维进行解决。
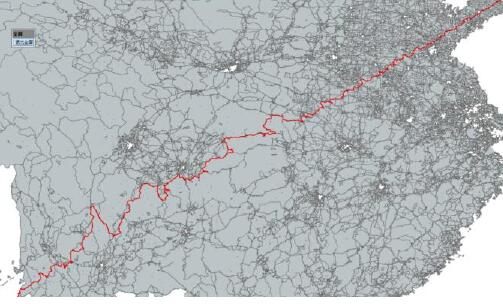
总结
通过GIS空间科学思维,将维度的升降运用到自然科学问题求解过程,往往会获得出其不意的效果,原因就在于升维代表无限可能,降维代表问题简化和解决。当前地理信息科学及其相关产业蓬勃发展,但理论基础是否牢固值得我们思考。本文将空间科学思维进行拓展,结合行业难题,阐述了如何利用思维革新创新科学研究的一种新尝试。项目当前已经取得一定进展,部分核心技术获得行业应用及政府科技奖项,未来尝试将空间科学思维拓展到非空间科学领域解决部分企业面临的相关技术难题,为地理信息科技工作者和科研人员提供新的思考。